

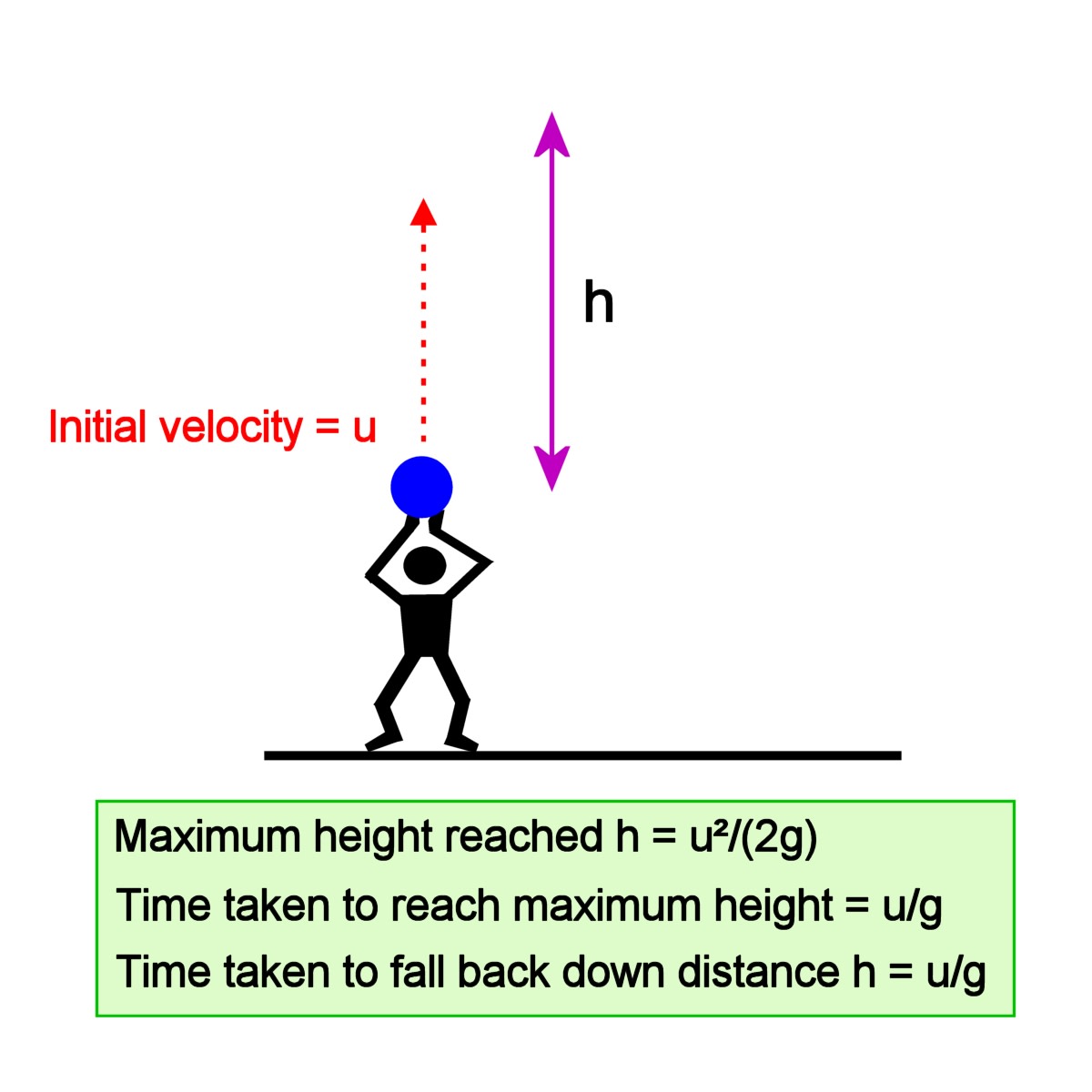
So this is the equation for the time required to reach the maximum height by the projectile. The initial velocity for the motion along Y-axis (as said above) is V 0sinθĬonsidering vertical motion along y-axis: Say the time required to reach this maximum height is t max. When the projectile reaches the maximum height then the velocity component along Y-axis i.e. Projectile motion: components of initial velocity V 0 Time to reach the Maximum Height by a projectile Hence we can say that trajectory of a projectile will follow a curve that is represented as Parabola. This is again an equation that represents Parabola. x 2/(V 0 cosθ) 2 As you see this can be rewritten in the form y = ax + bx 2 where a and b are constants. So once thrown at an angle (excluding right angle) with the horizontal, a projectile will follow a curved path named Parabola.Įquation of Trajectory of a projectile – a parabolaįrom equation 4 above, we get the trajectory path of a projectile as y = (tanθ) x – (1/2) g. So we can say that the trajectory or motion path of a projectile is a parabola. This is an equation representing parabola. So rewriting equation 4: y = ax + bx 2 where a and b are constants. In the above equation g, θ and V 0 are constant. Replacing t in equation 2 with the expression of t from equation 3: (Air resistance is taken as negligible)Īt time T = 0, there is no displacement along the X and Y axes.Īt time T=t, (i.e., for any time instant t) Displacement along X-axis = x= V 0x.t = (V 0 cosθ). The initial velocity component along X-axis = V 0x = V 0 cosθ and the initial velocity component along Y-axis = V 0y = V 0sinθ. Showing initial velocity V 0 and its components along X and Y axes for a projectile motion (Velocity components when time t =0) In the absence of air resistance, the path of the flight of a projectile will trace out the shape of a parabola as shown by the photograph in the figure below, taken with the aid of a stroboscope.
The trajectory of a projectile is the path that it follows during its flight. Projectile Motion Derivation of equation of path | Projectile Motion derivation class 11 Students of Class 11 from boards like ISC, CBSE, and state boards will find this one useful. We will cover here Projectile Motion Derivation to derive a couple of equations or formulas like:ġ> derivation of the projectile path equation (or trajectory equation derivation for a projectile)Ģ> derivation of the formula for time to reach the maximum heightģ> total time of flight – formula derivationĤ> Maximum height of a projectile – formula derivation andĥ> derivation of the formula for the horizontal range of a projectile In the next sections, we will discuss and derive a couple of projectile motion equations.ĭerivation of Projectile Motion Equations One component is along a horizontal direction without any acceleration (as no force acting in this direction) and the other along the vertical direction with constant acceleration due to the force of gravity (considering air resistance as negligible). The motion of a projected object in flight is known as projectile motion which is a result of 2 separate simultaneously occurring components of motions.
For example, the motions of a cricket ball, baseball. When an object is in flight after being projected or thrown then that object is called a projectile and this motion is called Projectile Motion.

Projectile & Projectile Motion – definitions Projectile definition


 0 kommentar(er)
0 kommentar(er)
